Distance-generalized Core Decomposition
Distance-generalized Core Decomposition
A summary of the SIGMOD 2019 research paper by Francesco Bonchi, Arijit Khan, and Lorenzo Severini
A summary of the SIGMOD 2019 research paper by Francesco Bonchi, Arijit Khan, and Lorenzo Severini
Background: Extracting dense structures from large graphs has emerged
as a key graph-mining primitive in a variety of application
scenarios, ranging from web mining, to biology,
and finance. Many different definitions of dense subgraphs have been proposed (e.g., cliques, n-cliques, n-clans,
k-plexes, f-groups, n-clubs, lambda sets), but most of them are NP-hard or at least quadratic. In this respect, the concept of
core decomposition is particularly appealing because (i) it can
be computed in linear time, and (ii) it is related to
many of the various definitions of a dense subgraph and it
can be used to speed-up or approximate their computation.
The k-core of a graph is defined as a maximal subgraph in
which every vertex is connected to at least k other vertices
within that subgraph. The set of all k-cores of a graph, for
each k, forms its core decomposition. The core index of a
vertex v is the maximal k for which v belongs to the k-core.
While core decomposition is based on the number of immediate connections that a vertex has within a subgraph
(its degree), the importance of studying network structures
beyond the horizon of the distance-1 neighborhood of a vertex is well established since several decades, especially in
social sciences [1]. Following this observation, in this paper
we introduce an important generalization of the notion of
core decomposition. Looking through the lens of shortest-path distance, one can see the degree of a vertex v as the
number of vertices in the graph which have distance ≤ 1
from v, or equivalently, the size of the 1-neighborhood of
v. From this perspective, a natural generalization is to consider a distance threshold h > 1. This leads smoothly to
the notions of h-neighborhood, h-degree, and in turn, to the
distance-generalized notion of (k,h)-core, i.e., the maximal
subgraph in which every vertex has at least k other vertices at distance ≤ h within that subgraph. As we formally
prove in this work, the (k,h)-core is unique and it is contained in
the (k − 1,h)-core: these facts allow us to define the notion
of distance-generalized core decomposition.
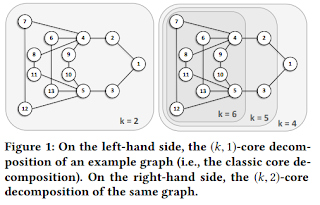
Figure 1 shows the differences between the classic core decomposition (on the left side) and the (k, 2)-core
decomposition (on the right side). For this example graph, the
classic core decomposition (i.e., the (k, 1)-core decomposition
in our setting) puts all the vertices in core k = 2. On the contrary, by considering distance-2 neighborhood, the (k, 2)-core
decomposition is able to capture structural differences among
the vertices, thus providing a finer-grained analysis. In particular, it allows detecting the fact that the vertices from 4 to
13 form a denser and more structured region (the (6, 2)-core),
while vertices 2 and 3 are in the (5, 2)-core, and vertex 1 only
belongs to the (4, 2)-core.
Why Core Decomposition of Power Graph Does Not Work? One could think to obtain the distance-generalized (k,h)-core decomposition, by first computing the h-power of the input graph (as in Figure 2), and then applying the state-of-the-art algorithms for core decomposition. However, this does not provide the correct decomposition, as shown next. Figure 2 shows the power-graph G^2 of the graph in Figure 1. We can observe that according to the classic core decomposition of G^2 , the vertices 2 and 3 have core-index 6, while in the (k, 2)-core decomposition of G (right side of Figure 1) they have core-index 5. This is due to the fact that in G^2, vertices 2 and 3 becomes adjacent due to vertex 1, but this vertex does not belong to the (5, 2)-core.
Challenges: In the classic core decomposition, when a vertex is removed, the degree of its neighbors is decreased by 1: this observation allows several optimizations which makes the classic case easy to compute and to scale [2, 3, 4, 5, 6, 7]. Instead, in the generalized (k,h)-core decomposition the removal of a vertex can decrease the h-degree of some of its h-neighbors by more than one. This is the reason why the idea of decomposing the h-power graph does not work, and it is also the main reason why distance-generalized core decomposition (h > 1) is much harder to compute than standard core decomposition (h = 1). In fact, when a vertex is removed, we need to compute again the h-degree of a large number of vertices, i.e., we need a large number of h-bounded BFS traversals.
Algorithmic Contribution: In spite of such challenges, we devise efficient algorithms. As a baseline, we first extend the state-of-the-art Batagelj and Zaveršnik’s algorithm [2] to deal with (k,h)-core decomposition (we dub the algorithm h-BZ). Next, we exploit a lower bound on the core-index of a vertex to avoid a large number of useless h-degree re-computations. We call this algorithm h-LB. Finally, we propose an algorithm that further improves efficiency by computing an upper bound and processing the vertices with larger h-degrees as early as possible (dubbed h-LB+UB). In order to scale to larger graphs we also exploit multi-threading provided by modern architectures to parallelize the computations of h-degrees.
Applications: We show that distance-generalized core decomposition generalizes many of the nice properties of the classic core decomposition, e.g., its connection with the notion of distance-generalized chromatic number, or its usefulness in speeding-up or approximating distance-generalized notions of dense structures, such as h-club, (distance-generalized) densest subgraph and community search problems (i.e., cocktail party) [8]. We also show that it is very informative and performs well as a heuristic for selecting landmarks to build shortest-path-distance oracles.
Why Core Decomposition of Power Graph Does Not Work? One could think to obtain the distance-generalized (k,h)-core decomposition, by first computing the h-power of the input graph (as in Figure 2), and then applying the state-of-the-art algorithms for core decomposition. However, this does not provide the correct decomposition, as shown next. Figure 2 shows the power-graph G^2 of the graph in Figure 1. We can observe that according to the classic core decomposition of G^2 , the vertices 2 and 3 have core-index 6, while in the (k, 2)-core decomposition of G (right side of Figure 1) they have core-index 5. This is due to the fact that in G^2, vertices 2 and 3 becomes adjacent due to vertex 1, but this vertex does not belong to the (5, 2)-core.
Challenges: In the classic core decomposition, when a vertex is removed, the degree of its neighbors is decreased by 1: this observation allows several optimizations which makes the classic case easy to compute and to scale [2, 3, 4, 5, 6, 7]. Instead, in the generalized (k,h)-core decomposition the removal of a vertex can decrease the h-degree of some of its h-neighbors by more than one. This is the reason why the idea of decomposing the h-power graph does not work, and it is also the main reason why distance-generalized core decomposition (h > 1) is much harder to compute than standard core decomposition (h = 1). In fact, when a vertex is removed, we need to compute again the h-degree of a large number of vertices, i.e., we need a large number of h-bounded BFS traversals.
Algorithmic Contribution: In spite of such challenges, we devise efficient algorithms. As a baseline, we first extend the state-of-the-art Batagelj and Zaveršnik’s algorithm [2] to deal with (k,h)-core decomposition (we dub the algorithm h-BZ). Next, we exploit a lower bound on the core-index of a vertex to avoid a large number of useless h-degree re-computations. We call this algorithm h-LB. Finally, we propose an algorithm that further improves efficiency by computing an upper bound and processing the vertices with larger h-degrees as early as possible (dubbed h-LB+UB). In order to scale to larger graphs we also exploit multi-threading provided by modern architectures to parallelize the computations of h-degrees.
Applications: We show that distance-generalized core decomposition generalizes many of the nice properties of the classic core decomposition, e.g., its connection with the notion of distance-generalized chromatic number, or its usefulness in speeding-up or approximating distance-generalized notions of dense structures, such as h-club, (distance-generalized) densest subgraph and community search problems (i.e., cocktail party) [8]. We also show that it is very informative and performs well as a heuristic for selecting landmarks to build shortest-path-distance oracles.
[Reference]
[1] R. Luce. Connectivity and Generalized Cliques in Sociometric Group Structure. Psychometrika, 15(2):169–190, 1950.
[2] V. Batagelj and M. Zaveršnik. Fast Algorithms for Determining (Generalized) Core Groups in Social Networks. Advances in Data Analysis and Classification, 5(2):129–145, 2011.
[3] J. Cheng, Y. Ke, S. Chu, and M. T. Özsu. Efficient core decomposition in massive networks. In ICDE, 2011.
[4] W. Khaouid, M. Barsky, V. Srinivasan, and A. Thomo. K-core decomposition of large networks on a single pc. PVLDB, 9(1):13–23, 2015.
[5] A. Montresor, F. D. Pellegrini, and D. Miorandi. Distributed k-Core Decomposition. TPDS, 24(2), 2013.
[6] K. Pechlivanidou, D. Katsaros, and L. Tassiulas. MapReduce-Based Distributed K-Shell Decomposition for Online Social Networks. In SERVICES, 2014.
[7] A. E. Sariyüce, B. Gedik, G. Jacques-Silva, K. Wu, and Ü. V. Çatalyürek. Streaming Algorithms for k-Core Decomposition. PVLDB, 6(6), 2013.
[8] M. Sozio and A. Gionis. The community-search problem and how to plan a successful cocktail party. In KDD, 2010.


Comments
Post a Comment