Big Graph Live

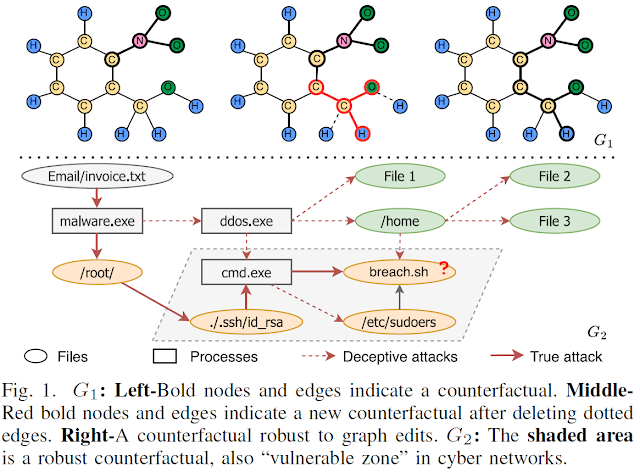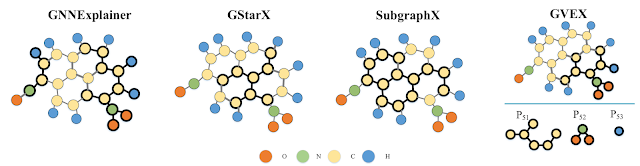
View-based Explanations for Graph Neural Networks A summary of the SIGMOD 2024 research  paper  by Tingyang Chen, Dazhuo Qiu, Yinghui Wu, Arijit Khan, Xiangyu Ke, and Yunjun Gao Background [Graph Classification, Graph Neural Networks, and Explainability].  Graph classification is essential for several real-world tasks such as drug discovery, text classification, and recommender system [1, 2, 3]. The rising graph neural networks (GNNs) have exhibited great potential in graph classification across many real domains, e.g., social networks, chemistry, and biology [4, 5, 6, 7]. Given a database G as a set of graphs, and a set of class labels Ł, GNN-based graph classification aims to learn a GNN as a classifier M, such that each graph 𝐺 ∈ G is assigned a correct label M ( 𝐺 ) ∈ Ł . GNNs are “black-box” — it is inherently difficult to understand which aspects of the input data drive the decisions of the network. Explainability can improve the model’s transparency related to fairnes

Generating Robust Counterfactual Witnesses for Graph Neural Networks A summary of the ICDE 2024 research  paper  by Dazhuo Qiu, Mengying Wang, Arijit Khan, and Yinghui Wu Background [Graph Neural Networks, Node Classification, and Explainability]:  Graph neural networks (GNNs) are deep learning models designed to tackle graph-related tasks in an end-to-end manner [1]. Notable variants of GNNs include graph convolution networks (GCNs) [2], attention networks (GATs) [3], graph isomorphism networks (GINs) [4], APPNP [10], and GraphSAGE [5]). Message-passing based GNNs share a similar feature learning paradigm: for each node, update node features by aggregating neighbor counterparts. The features can then be converted into labels or probabilistic scores for specific tasks. GNNs have demonstrated their efficacy on various tasks, including node and graph classification [2], [4], [6], [7], [8], and link prediction [9]. Given a graph G and a set of test nodes V T , a GNN-based node class