Notes on Expressibility of
Vertex Centric Graph Processing Paradigm
A summary of the IEEE BigData 2018 research paper by Siyuan Liu and Arijit Khan
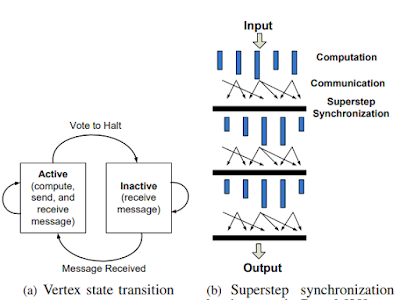
We study the vertex-centric (VC) paradigm for distributed graph processing, popularized by Google’s Pregel system [1]. In Pregel, which was inspired by the Bulk Synchronous Parallel (BSP) model [2], graph algorithms are expressed as a sequence of iterations called supersteps (Figure 1). Each superstep is an atomic unit of parallel computation. During a superstep, Pregel executes a user-defined function for each vertex in parallel. The user-defined function specifies the operation at a single vertex v and at a single superstep S. The supersteps are globally synchronous among all vertices, and messages are usually sent along the outgoing edges from each vertex. In 2012, Yahoo! launched the Apache Giraph [3] as an open-source project, which clones the concepts of Pregel. Since then, there were several attempts to implement many graph algorithms in a vertex-centric framework, as well as efforts to design optimization techniques for improving their efficiency. Many follow up works experimentally compared the efficiency and scalability of existing VC systems (for a survey, see [10], [11], [12], [13]). However, to the best of our knowledge, there has not been any systematic study to analyze the expressibility of the VC paradigm itself.
Fig. 1: Vertex-Centric paradigm
In this work, we investigate some of the fundamental limitations of the vertex-centric paradigm itself, by implementing a few distributed graph algorithms that are difficult to be expressed in the VC paradigm. Several graph problems have multiple distributed algorithms, which vary in their efficiency. We observe that not all distributed algorithms of a graph problem can be implemented effectively in the vertex-centric framework. In particular, we focus on two specific classes of algorithms: bucketing-based and multi-phased.
Bucketing-based refers to an algorithm that relies on a bucket structure to define priorities of vertices. Vertices are processed in batch from the highest priority vertices to lowest priority vertices. Vertices can be added and removed from buckets during execution to update their priorities. Example algorithms in this class include ∆-Stepping algorithm [4] for single-source shortest path, weighted BFS [5], k-core [6], and approximate set cover [7].
Multi-phased implies those algorithms which consists of several distinct phases. Each phase itself may be iterative. However, overall the algorithm’s execution follows the predefined order of phases. Example algorithms that fall under this category include distributed Brandes’ algorithm [8] for betweenness centrality, finding bi-connected and strongly connected components [9].
We find that often the more efficient distributed algorithm of a graph problem under the above two categories cannot be effectively implemented in the vertex-centric paradigm. We highlight the key expressibility limitations (e.g., more work, many active vertices, large message overheads, etc.) of VC paradigm in regards to both bucketing-based and multi-phase algorithms. We conduct extensive experiments to demonstrate these expressibility challenges specific to vertex-centric paradigm, while also presenting that such bottlenecks do not exist in traditional message passing interface (MPI) distributed systems.
We conclude by discussing our recommendations on the road ahead for VC systems, such as (1) directly incorporating priority-based data structures (e.g., buckets) in each worker node, that will permit defining and dynamically updating priorities of vertices, and (2) providing more control to the master node, so that it can re-activate vertices during phase changes.
[Reference]
A summary of the IEEE BigData 2018 research paper by Siyuan Liu and Arijit Khan
We study the vertex-centric (VC) paradigm for distributed graph processing, popularized by Google’s Pregel system [1]. In Pregel, which was inspired by the Bulk Synchronous Parallel (BSP) model [2], graph algorithms are expressed as a sequence of iterations called supersteps (Figure 1). Each superstep is an atomic unit of parallel computation. During a superstep, Pregel executes a user-defined function for each vertex in parallel. The user-defined function specifies the operation at a single vertex v and at a single superstep S. The supersteps are globally synchronous among all vertices, and messages are usually sent along the outgoing edges from each vertex. In 2012, Yahoo! launched the Apache Giraph [3] as an open-source project, which clones the concepts of Pregel. Since then, there were several attempts to implement many graph algorithms in a vertex-centric framework, as well as efforts to design optimization techniques for improving their efficiency. Many follow up works experimentally compared the efficiency and scalability of existing VC systems (for a survey, see [10], [11], [12], [13]). However, to the best of our knowledge, there has not been any systematic study to analyze the expressibility of the VC paradigm itself.
In this work, we investigate some of the fundamental limitations of the vertex-centric paradigm itself, by implementing a few distributed graph algorithms that are difficult to be expressed in the VC paradigm. Several graph problems have multiple distributed algorithms, which vary in their efficiency. We observe that not all distributed algorithms of a graph problem can be implemented effectively in the vertex-centric framework. In particular, we focus on two specific classes of algorithms: bucketing-based and multi-phased.
Bucketing-based refers to an algorithm that relies on a bucket structure to define priorities of vertices. Vertices are processed in batch from the highest priority vertices to lowest priority vertices. Vertices can be added and removed from buckets during execution to update their priorities. Example algorithms in this class include ∆-Stepping algorithm [4] for single-source shortest path, weighted BFS [5], k-core [6], and approximate set cover [7].
Multi-phased implies those algorithms which consists of several distinct phases. Each phase itself may be iterative. However, overall the algorithm’s execution follows the predefined order of phases. Example algorithms that fall under this category include distributed Brandes’ algorithm [8] for betweenness centrality, finding bi-connected and strongly connected components [9].
We find that often the more efficient distributed algorithm of a graph problem under the above two categories cannot be effectively implemented in the vertex-centric paradigm. We highlight the key expressibility limitations (e.g., more work, many active vertices, large message overheads, etc.) of VC paradigm in regards to both bucketing-based and multi-phase algorithms. We conduct extensive experiments to demonstrate these expressibility challenges specific to vertex-centric paradigm, while also presenting that such bottlenecks do not exist in traditional message passing interface (MPI) distributed systems.
We conclude by discussing our recommendations on the road ahead for VC systems, such as (1) directly incorporating priority-based data structures (e.g., buckets) in each worker node, that will permit defining and dynamically updating priorities of vertices, and (2) providing more control to the master node, so that it can re-activate vertices during phase changes.
[1] G. Malewicz, M. H. Austern,
A. J. Bik, J. C. Dehnert, I. Horn, N. Leiser, and G. Czajkowski. Pregel: A
System for Large-scale Graph Processing. In SIGMOD, 2010.
[2] L. G. Valiant. A Bridging
Model for Parallel Computation. Commun. ACM, 33(8):103–111, 1990.
[4] U. Meyer and P. Sanders. ∆--stepping:
A parallelizable shortest path algorithm. J. Algorithms, 49(1):114–152, 2003.
[5] R. Dial Algorithm 360:
Shortest-path forest with topological ordering [H]. Commun. ACM,
12(11):632–633, 1969.
[6] L. Dhulipala, G. Blelloch, J.
Shun Julienne: A framework for parallel graph algorithms using work-efficient
bucketing. In SPAA, 2017.
[7] G. Blelloch, R. Peng, K.
Tangwongsan Linear-work greedy parallel approximate set cover and variants. In
SPAA, 2011.
[8] U. Brandes. A Faster
Algorithm for Betweenness Centrality. Journal of Mathematical Sociology,
25(163), 2001.
[9] D. Yan, J. Cheng, K. Xing, Y.
Lu, W. Ng, and Y. Bu. Pregel Algorithms for Graph Connectivity Problems with
Performance Guarantees. PVLDB, 7(14):1821–1832, 2014.
[10] M. Han, K. Daudjee, K.
Ammar, M. T. Ozsu, X. Wang, and T. Jin. An Experimental Comparison of
Pregel-like Graph Processing Systems. PVLDB, 7(12):1047–1058, 2014.
[11] A. Khan and S. Elnikety.
Systems for Big-Graphs. PVLDB, 7(13):1709– 1710, 2014.
[12] R. R. McCune, T. Weninger,
and G. Madey. Thinking Like a Vertex: A Survey of Vertex-Centric Frameworks for
Large-Scale Distributed Graph Processing. ACM Comput. Surv., 48(2):25:1–25:39,
2015.
[13] D. Yan, Y. Bu, Y. Tian, A.
Deshpande, and J. Cheng. Big Graph Analytics Systems. In SIGMOD, 2016.
Comments
Post a Comment