Big Graph Live

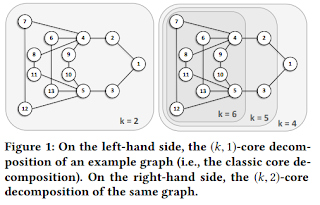
Distance-generalized Core Decomposition A summary of the SIGMOD 2019 research  paper  by  Francesco Bonchi, Arijit Khan, and Lorenzo Severini Background: Extracting dense structures from large graphs has emerged as a key graph-mining primitive in a variety of application scenarios, ranging from web mining, to biology, and finance. Many different definitions of dense subgraphs have been proposed (e.g., cliques, n-cliques, n-clans, k-plexes, f-groups, n-clubs, lambda sets), but most of them are NP-hard or at least quadratic. In this respect, the concept of core decomposition is particularly appealing because (i) it can be computed in linear time, and (ii) it is related to many of the various definitions of a dense subgraph and it can be used to speed-up or approximate their computation. The k-core of a graph is defined as a maximal subgraph in which every vertex is connected to at least k other vertices within that subgraph. The set of all k-cores of a graph,...

An In-Depth Comparison of s-t Reliability Algorithms over Uncertain Graphs A summary of the PVLDB 2019 research  paper  by Xiangyu Ke, Arijit Khan, and Leroy Lim Hong Quan Uncertain, or probabilistic, graphs have been increasingly used to represent noisy linked data in many emerging applications, and have recently attracted the attention of the database research community [7]. A fundamental problem on uncertain graphs is the s-t reliability, which measures the probability that a target node t is reachable from a source node s in a probabilistic (or uncertain) graph, i.e., a graph where every edge is assigned a probability of existence.  This s - t reliability estimation has been used in many applications such as measuring the quality of connections between two terminals in a sensor network, finding other proteins that are highly probable to be connected with a specific protein in a protein-protein interaction (PPI) network, identifying highly reliable peers cont...