On Smart Query Routing: For Distributed Graph Querying with Decoupled Storage

On Smart Query Routing: For Distributed Graph Querying with Decoupled Storage

A summary of the USENIX ATC 2018 research paper by Arijit Khan, Gustavo Segovia, and Donald Kossmann

Background: Distributed Graph Querying & Graph Partitioning

Graphs with millions of nodes and billions of edges are ubiquitous to represent highly interconnected structures including the World Wide Web, social networks, knowledge graphs, genome and scientific databases, medical and government records. To support online search and query services (possibly from many clients) with low latency and high throughput, data centers and cloud operators consider scale-out solutions, in which the graph and its data are partitioned horizontally across cheap commodity servers. We assume that the graph topology and the data associated with nodes and edges are co-located, since they are often accessed together. Keeping with the modern database trends to support low-latency operations, we target a fully in-memory system, and use disks only for durability.

                                 

Fig. 1: State-of-the-art distributed graph querying systems (e.g., SEDGE [1], Trinity [2], Horton [3])

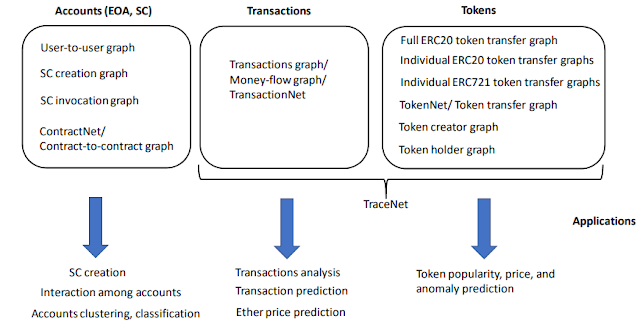
For efficiently answering online queries in a distributed environment, state-of-the-art systems (e.g., SEDGE[1], Horton[2], Trinity [3]) first partition the graph, and then place each partition on a separate server, where query answering over that partition takes place (Fig. 1). Since the server which contains the query node can only handle that request, the router maintains a fixed routing table (or, a fixed routing strategy, e.g., modulo hashing). Hence, these systems are less flexible with respect to query routing and fault tolerance, e.g., adding more machines will require updating the data partition and/or the routing table. Besides, an effective graph partitioning in these systems must achieve: (1) workload balancing to maximize parallelism, and (2) locality of data access to minimize network communication. It has been demonstrated in the literature that sophisticated partitioning schemes improve the performance of graph querying, compared to an inexpensive hash partitioning. Due to power-law degree distribution of real-world graphs, it is difficult to get high-quality partitions. Besides, a one-time partitioning cannot cope with later updates to graph structure or variations in query workloads. Several graph re-partitioning and replication-based strategies were proposed. However, online monitoring of workload changes, re-partitioning of the graph topology, and migration of graph data across servers are expensive; and they reduce the efficiency and throughput of online querying.

A Decoupled Graph Querying System: Pros and Cons

In contrast to existing systems, we consider a different architecture, which relies less on an effective graph partitioning. Instead, we decouple query processing and graph storage into two separate tiers (Fig. 2). This decoupling happens at a logical level. As an example, query processors can be different physical machines than storage servers. On the other hand, the same physical machine can also run a query processing daemon, together with storing a graph partition in its main memory as a storage server. However, the logical separation between the two layers is critical in our design.

In a decoupled framework, the graph is partitioned across servers allocated to the storage tier, and these storage servers hold the graph data in their main memory. Since a query processor is no longer assigned any fixed part of the graph, it is equally capable of handling any request, thus facilitating load balancing and fault tolerance. At the same time, the query router can send a request to any of the query processors, which adds more flexibility to query routing, e.g., more query processors can be added (or, a query processor that is down can be replaced) without affecting the routing strategy. Another benefit due to decoupled design is that each tier can be scaled-up independently. If a certain workload is processing intensive, more servers could be allocated to the processing tier. On the contrary, if the graph size increases over time, more servers can be added in the storage  tier. This decoupled architecture, being generic, can be employed in many existing graph querying systems.

Fig. 2: Decoupled architecture for graph querying

The idea of decoupling has been effectively used in the past. Facebook implemented a fast caching layer, Memcached on top of a graph database that scales the performance of graph query answering [4]. Google’s F1 [5] and ScaleDB [6] are based on a decoupling principle for scalability. Recently, Loesing et. al. [7] and Binnig et. al. [8] demonstrated the benefits of a decoupled, shared-data architecture, together with low latency and high throughput Infiniband network. Shalita et. al. [9] employed decoupling for an optimal assignment of HTTP requests over a distributed graph storage.

However, we must also consider the drawbacks of having the graph storage apart. First, query processors may need to communicate with the storage tier via the network. This includes an additional penalty to the response time for answering a query. Second, it is possible that this design causes high contention rates on either the network, storage tier, or both.

Our contribution lies in designing a smart query routing logic to utilize the cache of query processors over such decoupled architecture. Achieving more cache hits is critical in a decoupled architecture, in order to reduce the communication among query processors and storage servers. However, this is a non-trivial problem, e.g., exploiting cache locality and balancing workloads are conflicting in nature. For example, to achieve maximum cache locality, the router can send all the queries to the same processor (assuming no cache eviction happens). However, the workload of the processors will be highly imbalanced, resulting  in lower throughput. In addition, graph workloads are significantly different from traditional database applications. The interconnected nature of graph data results in poor locality, and each query usually accesses multiple neighboring nodes spreading across the distributed storage. Therefore, to maximize cache hit rates at query processors, it is not sufficient to only route the queries on same nodes to the same processor. Rather, successive queries on neighboring nodes should also be routed to the same processor, since the neighborhoods of two nearby nodes may significantly overlap. To the best of our knowledge, such smart query routing schemes for effectively leveraging the cache contents were not considered in existing graph querying systems.

h-Hop Graph Traversal Queries:

In this work, we consider online, h-hop queries that explore a small region of the entire graph, and require fast response time. These queries usually start with a query node, and traverse its neighboring nodes up to a certain number of hops (i.e., h = 2, 3). Examples include h-hop neighbor aggregation, h-step random walk with restart, h-hop reachability, etc. These queries are often used as the basis for more complex graph operations. For example, neighborhood aggregation is critical for node labeling and classification, that is, the label of an unlabeled node could be assigned as the most frequent label which is present within its h-hop neighborhood. The h-step random walk is useful in expert finding, ranking, discovering functional modules, complexes, and pathways. 

Smart Graph Query Routing Schemes:

We identify the following objectives that a smart graph query routing scheme must satisfy.

1. Leverage each processor’s cached data. Let us consider t successive queries received by the router. The router will send them to query processors in a way such that the average number of cache hits at the processors is maximized. This, in turn, reduces the average query processing latency. However, as stated earlier, to achieve maximum cache hits, it will not be sufficient to only route the queries on same nodes to the same processor. Rather, successive queries on neighboring nodes should also be routed to the same processor, since the neighborhoods of two nearby nodes may significantly overlap.

2. Balance workload even if skewed or contains hotspot. As earlier, let us consider a set of t successive queries. A na¨ıve approach will be to ensure that each query processor receives equal number of queries, e.g., a round-robin way of query dispatching by the router. However, each query might have a different workload, and would require a different processing time. We, therefore, aim at maximizing the overall throughput via query stealing, which automatically balances the workload across query processors.

3. Make fast routing decisions. The average time at the router to dispatch a query should be minimized, ideally a small constant time, or much smaller than O(n), where n is the number of nodes in the input graph. This reduces the query processing latency.

4. Have low storage overhead in the router. The router may store auxiliary data to enable fast routing decisions. However, this additional storage overhead must be a small fraction compared to the graph size.

Based on the above requirements, we design two smart routing strategies: landmark routing and graph embed routing. Kleinberg et. al. [10] discussed the problem of approximating graph distances using a small set of beacons (i.e., landmarks). Graph embedding algorithms, on the other hand, place nodes at points on some surface such that the inherent graph structure is preserved [11, 12]. In this post, we briefly discuss our graph embedding-based query routing strategy: We embed a graph into a lower D-dimensional Euclidean space such that the hop-count distance between graph nodes are approximately preserved via their Euclidean distance (Fig. 3).  Since each node receives D co-ordinates, it requires total O(nD) space in the router, which is linear in the number of nodes. 

Fig. 3: Example of graph embedding in 2D Euclidean plane

In embed routing, the router has access to each node's co-ordinates. By keeping an average of the query nodes’ co-ordinates that it sent to each processor, it is able to infer the cache contents in these processors. As a consequence, the router finds the distance between a query node u and a processor p, denoted as d(u, p), and defined as the distance of the query node's co-ordinates to the historical mean of the processor's cache contents. As recent queries are more likely to influence the cache contents due to LRU eviction policy, we use the exponential moving average (i.e., recent queries are given more weight) to compute the mean of the processor's cache contents. We select the processor with the smallest d(u, p) distance. Observe that the routing decision time is only O(PD), P being the number of processors and D the number of dimensions. Furthermore, the distance metric d(u, p) is useful not only in finding the best processor for a certain query, but it can also be used for load balancing, dealing with workload skew, and hotspots. As an example, let us assume that the closest processor for a certain query is busy, or is currently down. Since the distance metric gives us distances to all processors, the router is able to select the second, third, or so on closest processor (query stealing). This form of load balancing impacts nearby query nodes in the same way, hence they are routed to the same query processor, thereby leveraging neighborhood-based locality.

Our experiments with several real-world, large graphs demonstrate that the proposed framework gRouting, even with simple hash partitioning, achieves up to an order of magnitude better query throughput compared to existing distributed graph systems that employ expensive graph partitioning and re-partitioning strategies. In addition to workload balancing and deployment flexibility, gRouting is able to provide linear scalability in throughput with more number of query processors, works well in the presence of query hotspots, and is also adaptive to workload changes and graph updates.

For more information, click here for our paper.
Blog post contributed by: Arijit Khan

[Reference]

[1] YANG, S., YAN, X., ZONG, B., AND KHAN, A. Towards Effective Partition Management for Large Graphs. In SIGMOD (2012).

[2] SHAO, B., WANG, H., AND LI, Y. Trinity: A Distributed Graph Engine on a Memory Cloud. In SIGMOD (2013).

[3] SARWAT, M., ELNIKETY, S., HE, Y., AND MOKBEL, M. F. Horton+: A Distributed System for Processing Declarative Reachability Queries over Partitioned Graphs. PVLDB 6, 14 (2013). 

[4] NISHTALA, R., FUGAL, H., GRIMM, S., KWIATKOWSKI, M., LEE, H., LI, H. C., MCELROY, R., PALECZNY, M., PEEK, D., SAAB, P., STAFFORD, D., TUNG, T., AND VENKATARAMANI, V. Scaling Memcache at Facebook. In NSDI (2013).

[5] SHUTE, J., VINGRALEK, R., SAMWEL, B., HANDY, B., WHIPKEY, C., ROLLINS, E., OANCEA, M., LITTLEFIELD, K., MENESTRINA, D., ELLNER, S., CIESLEWICZ, J., RAE, I., STANCESCU, T., AND APTE, H. F1: A Distributed SQL Database That Scales. PVLDB 6, 11 (2013).

[6] http://scaledb.com/pdfs/TechnicalOverview.pdf

[7] LOESING, S., PILMAN, M., ETTER, T., AND KOSSMANN, D. On the Design and Scalability of Distributed Shared-Data Databases. In SIGMOD (2015).

[8] BINNIG, C., CROTTY, A., GALAKATOS, A., KRASKA, T., AND ZAMANIAN, E. The End of Slow Networks: It’s Time for a Redesign. PVLDB 9, 7 (2016).

[9] SHALITA, A., KARRER, B., KABILJO, I., SHARMA, A., PRESTA, A., ADCOCK, A., KLLAPI, H., AND STUMM, M. Social Hash: An Assignment Framework for Optimizing Distributed Systems Operations on Social Networks. In NSDI (2016).

[10] KLEINBERG, J., SLIVKINS, A., AND WEXLER, T. Triangulation and Embedding Using Small Sets of Beacons. J. ACM 56, 6 (2009). 

[11] DABEK, F., COX, R., KAASHOEK, F., AND MORRIS, R. Vivaldi: A Decentralized Network Coordinate System. In SIGCOMM (2004).

[12] ZHAO, X., SALA, A., WILSON, C., ZHENG, H., AND ZHAO, B. Y. Orion: Shortest Path Estimation for Large Social Graphs. In WOSN (2010).