Measurements, Analyses, and Insights on the Entire Ethereum Blockchain Network

 Voting-based Opinion Maximization

A summary of the IEEE International Conference on Data Engineering (ICDE) 2023 research paper by Arkaprava Saha, Xiangyu Ke, Arijit Khan, and Laks V. S. Lakshmanan

Background: We investigate the novel problem of voting-based opinion maximization in a social network. In the presence of competing campaigns, we find a given number of seed nodes for a target campaigner that maximize a voting-based score for the target campaigner at a given time-horizon. Our work bridges two different paradigms: (1) seed selection for opinion formation and diffusion till a given finite time-horizon, and (2) voting-based winning criteria (e.g., plurality, Copeland) with multiple campaigners.

The classic influence maximization (IM) problem [1, 2] identifies the top-k seed users in a social network to maximize the expected number of influenced users in the network, starting from those seed nodes and following an influence diffusion model, e.g., independent cascade (IC) and linear threshold (LT). Several works also focus on competitive influence maximization, which aim to find the seed set that maximizes the influence spread for a particular campaigner relative to the others or maximally blocks the diffusion of a competitor [3, 4, 5, 6, 7, 8, 9, 10].

However, prior works on IM have two major limitations in modeling real-world opinion formation and spreading. First, they consider maximizing the expected number of users adopting a specific campaign, assuming that the reaction of each user to the campaign is binary (adopt or not). In reality, a user may not be completely opposed to the competing opinions, although the user could have a preference for one opinion, where the degree of preference could vary among users. This scenario can be modeled by allowing the opinion of a user for each campaign to be a real number in [0, 1]. Second, in the IC and LT models, a user’s choice is frozen upon one-time activation – not permitting to switch opinions later. While this is realistic when purchasing one of the many competing products due to the user’s limited budget, it is insufficient for modeling opinion formation and manipulation over time, e.g., in scenarios like paid movie services, elections, social issues, where a user’s opinion is highly likely to change over time.

The Problem Studied: we deviate from the classic influence diffusion (e.g., IC and LT models) and investigate the problem of opinion maximization by employing models rooted in opinion formation and diffusion, e.g., DeGroot [11] and Friedkin-Johnsen (FJ) [12, 13]. In these settings, each user in a network has a real-valued opinion about each campaign at every timestamp. For each campaign, the opinions of the users evolve over discrete timestamps according to an opinion diffusion model such as DeGroot or FJ.

Given a target campaign and a time-horizon (a future timestamp t), our problem is to select a seed set of size k for the target campaigner, so that the target campaigner’s odds of being the winner at the time-horizon t are as high as possible.

Since opinion values are non-binary, we require more sophisticated winning criteria than the expected influence spread employed in classic IM [1]. Voting offers a well-understood mechanism for determining winners in an election among campaigners by considering the preferences of users (“voters”) in a principled manner [27]. We investigate voting-based scores [14, 15, 16] such as aggregated opinion values of all users about a campaigner (cumulative), rank of the target campaigner relative to others for all users (plurality), or the number of campaigners against whom the target campaigner wins in one-on-one competitions (Copeland). These are natural choices based on voting theory when users have non-binary opinion values towards multiple competitors.

Our problem and solutions can be effective where users vote and the winner among multiple candidates is decided based on the election outcome. Examples include the presidential election, voting in the parliament, a plebiscite or a referendum (e.g., the referendum on the independence of Scotland) [17, 18], etc.

Existing works on finding the top-k seeds for opinion maximization [19, 20] are restricted to a single campaigner and consider neither a given finite time-horizon, nor voting-based scores with multiple competing campaigners. To the best of our knowledge, voting-based opinion maximization in the presence of multiple competing campaigns is a novel problem.

Our Solution Framework:

• Sandwich Approximation: Our problem is NP-hard and non-submodular under various voting scores. We, therefore, design bound functions for all our non-submodular scores to derive accuracy guarantees for the greedy algorithm via sandwich approximation [21].

• Random Walks: Computing opinion values at the time horizon via DeGroot/ FJ requires iterative matrix-vector multiplications, which is expensive. To improve the efficiency, we develop random walk and sketching-based computations with approximation guarantees. Random walks have been used earlier to improve the efficiency of matrix multiplication and PageRank computation [22, 23]. Different from them, we use random walks to find the k seed nodes maximizing a voting-based score by approximating the opinion values via the walks in k iterations. Also, we provide novel bounds on the number of walks required for each voting-based scoring function.

• Sketches: While sketches have been used in classic IM [24, 25, 26], we use sketches for opinion computation. We adapt sketches for opinion diffusion models and voting-based scores, and derive non-trivial accuracy guarantees. Moreover, our sketches are simpler and less memory-consuming than RR-sets-based sketches [24, 25].

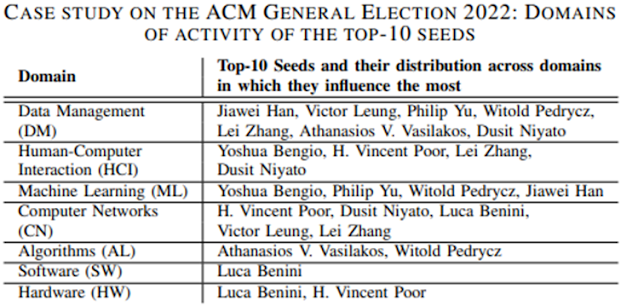
Case Study: We conduct a hypothetical case study about the ACM general election 2022. We observe that after including only the top-100 seeds, the number of users favoring our target candidate Joseph A. Konstan could have significantly increased from 13990 (21.8%) to 46433 (72.7%), which might have reversed the election result. In Table 1, we present 7 frequent research domains for the users who could have changed their preferred candidates, and show the top-10 seeds and the domains in which these seeds influence the most. Notice that a seed user may influence users from several domains. As Data Management (DM) is a common domain of both candidates (Joseph A. Konstan and Yannis E. Ioannidis), 7 out of the top-10 seeds are also active in the DM domain. Only 1- 2 seeds are from the Software (SW) and Hardware (HW) domains, since (1) the users in the SW domain already favor our target candidate more based on their initial opinions (thus introducing seeds who can influence users in this domain is not that useful); (2) the HW domain does not overlap with the DM domain. The numbers of seeds who influence the Human-Computer Interaction (HCI), Machine Learning (ML), and Computer Networks (CN) domains are higher, because (1) these domains have larger populations; (2) these domains have large overlaps with DM; and (3) the users in these domains initially prefer the competitor (Yannis E. Ioannidis) more, thus introducing seed nodes who can influence users in these domains is more helpful. Furthermore, we investigate the average distance between the candidates and those users who could have changed minds after introducing the seeds. 14.5% of them are closer to the target candidate, and 10.2% of them are closer to the competitors (about 2-hops away). The majority of these users (75.3%) are almost equidistant from both candidates (more than 3 hops away). This demonstrates that our solution focuses more on affecting the neutral users whose preferences are usually easier to switch, showcasing the usefulness of our problem and the effectiveness of our solution.

Table 1

For more information, click here for our paper.

References

[1] D. Kempe, J. Kleinberg, and E. Tardos, “Maximizing the spread of influence through a social network,” in Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2003, p. 137–146.

[2] P. Domingos and M. Richardson, “Mining the network value of customers,” in Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2001, p. 57–66.

[3] S. Bharathi, D. Kempe, and M. Salek, “Competitive influence maximization in social networks,” in International Workshop on Web and Internet Economics. Berlin, Heidelberg: Springer, 2007, pp. 306–311.

[4] T. Carnes, C. Nagarajan, S. M. Wild, and A. van Zuylen, “Maximizing influence in a competitive social network: A follower’s perspective,” in Proceedings of the 9th International Conference on Electronic Commerce, 2007, p. 351–360.

[5] X. He, G. Song, W. Chen, and Q. Jiang, “Influence blocking maximization in social networks under the competitive linear threshold model,” in Proceedings of the 2012 SIAM International Conference on Data Mining, 2012, pp. 463–474.

[6] Y. Lin and J. C. Lui, “Analyzing competitive influence maximization problems with partial information: An approximation algorithmic framework,” Performance Evaluation, vol. 91, pp. 187–204, 2015.

[7] M. Kahr, M. Leitner, M. Ruthmair, and M. Sinnl, “Benders decomposition for competitive influence maximization in (social) networks,” Omega, vol. 100, p. 102264, 2021.

[8] C. Budak, D. Agrawal, and A. El Abbadi, “Limiting the spread of misinformation in social networks,” in Proceedings of the 20th International Conference on World Wide Web, 2011, p. 665–674.

[9] W. Lu, F. Bonchi, A. Goyal, and L. V. Lakshmanan, “The bang for the buck: Fair competitive viral marketing from the host perspective,” in Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2013, pp. 928–936.

[10] A. Khan, B. Zehnder, and D. Kossmann, “Revenue maximization by viral marketing: A social network host’s perspective,” in 2016 IEEE 32nd International Conference on Data Engineering, 2016, pp. 37–48.

[11] M. H. DeGroot, “Reaching a consensus,” Journal of the American Statistical Association, vol. 69, no. 345, pp. 118–121, 1974.

[12] N. E. Friedkin and E. C. Johnsen, “Social influence and opinions,” Journal of Mathematical Sociology, vol. 15, no. 3-4, pp. 193–206, 1990.

[13] N. E. Friedkin and E. C. Johnsen, “Social influence networks and opinion.

[14] E. Pacuit, “Voting methods,” in The Stanford Encyclopedia of Philosophy. Stanford, CA, USA: Metaphysics Research Lab, Stanford University, 2019.

[15] W. Gaertner, A primer in social choice theory. Oxford, UK: Oxford University Press, 2006.

[16] P. C. Fishburn, “Paradoxes of voting,” The American Political Science Review, vol. 68, no. 2, pp. 537–546, 1974.

[17] B. S. Frey, “Direct democracy: politico-economic lessons from swiss experience,” The American Economic Review, vol. 84, no. 2, pp. 338– 342, 1994.

[18] P. Emerson, Decision-making in parliaments and referendums. Springer International Publishing, 2020, pp. 3–30.

[19] A. Gionis, E. Terzi, and P. Tsaparas, “Opinion maximization in social networks,” in Proceedings of the 2013 SIAM International Conference on Data Mining, 2013, pp. 387–395.

[20] R. Abebe, J. Kleinberg, D. Parkes, and C. E. Tsourakakis, “Opinion dynamics with varying susceptibility to persuasion,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2018, p. 1089–1098.

[21] W. Lu, W. Chen, and L. V. Lakshmanan, “From competition to complementarity: Comparative influence diffusion and maximization,” Proc. VLDB Endow., vol. 9, no. 2, p. 60–71, 2015.

[22] K. Avrachenkov, N. Litvak, D. Nemirovsky, and N. Osipova, “Monte carlo methods in pagerank computation: When one iteration is sufficient,” SIAM Journal on Numerical Analysis, vol. 45, no. 2, pp. 890–904, 2007.

[23] E. Cohen and D. D. Lewis, “Approximating matrix multiplication for pattern recognition tasks,” Journal of Algorithms, vol. 30, no. 2, pp. 211–252, 1999.

[24] Y. Tang, Y. Shi, and X. Xiao, “Influence maximization in near-linear time: A martingale approach,” in Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, 2015, p. 1539–1554.

[25] Y. Tang, X. Xiao, and Y. Shi, “Influence maximization: Near-optimal time complexity meets practical efficiency,” in Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, 2014, p. 75–86.

[26] C. Borgs, M. Brautbar, J. Chayes, and B. Lucier, “Maximizing social influence in nearly optimal time,” in Proceedings of the 2014 ACM-SIAM Symposium on Discrete Algorithms, 2014, pp. 946–957.

[27] S. Basu Roy, “RETURNING TOP-K : PREFERENCE AGGREGATION OR SORTITION, OR IS THERE A BETTER MIDDLE GROUND?” in ACM SIGMOD Blog, https://wp.sigmod.org/?p=3564.