Measurements, Analyses, and Insights on the Entire Ethereum Blockchain Network

Aggregate Queries on Knowledge Graphs: Fast Approximation with Semantic-aware Sampling

A summary of the IEEE ICDE 2022 research paper by Yuxiang Wang, Arijit Khan, Xiaoliang Xu, Jiahui Jin, Qifan Hong, and Tao Fu.

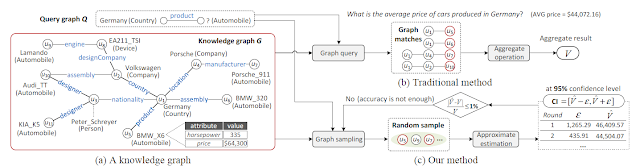
Background: Knowledge graphs (KGs), such as DBpedia [1], YAGO [2], Freebase [3], and NELL [4], manage large-scale and real-world facts as big graphs in a schema-flexible manner. The same kind of information can be represented as diverse substructures [5], [6]. This schema-flexible nature should be carefully considered in the study of KG querying. Consider the factoid query [7]: e.g., “Find all cars produced in Germany” (Q117 from QALD-4 benchmark [8]). Given the KG in Figure 1(a), we expect answers as all entities having type Automobile that satisfy the semantic relation product to the specific entity Germany, e.g., Audi TT (u10), BMW 320 (u6), etc. Notice that these correct answers are linked with Germany in structurally different ways in Figure 1(a), for instance, u10: Audi TT-assembly-Volkswagen-country-Germany; u6: BMW 320-assembly-Germany. This reflects the “schema-flexible” nature of a KG and we expect to find all the semantically similar answers for factoid queries.

Figure 1: (a) Each entity of this knowledge graph with type Automobile has many numerical attributes, including horsepower, price, etc. (b) The traditional method computes an aggregate result based on the graph matches via graph query. (c) Our method computes an approximate aggregate result with an accuracy guarantee in the form of confidence interval (CI) through a “sampling-estimation” model.

In this work, we focus on aggregate queries on a KG, e.g., “what is the average price of cars produced in Germany?” is an aggregate query to achieve AVG(price) of all the Automobiles that satisfy the semantic relation product to the specific entity Germany. We find that 31% queries from the real query log LinkedGeoData13 and 30% queries from the manually curated query set WikiData17 are aggregate queries [9]. Despite its importance, answering aggregate queries on KGs has received little attention in the literature.

Challenges: Aggregate queries can be supported based on factoid queries (Figure 1(b)), e.g., “Find all cars produced in Germany”, by applying an additional aggregate operation on factoid queries’ answers. However, this straightforward method is challenging because both the accuracy and efficiency of factoid query processing will seriously impact the performance of aggregate queries. For example, subgraph isomorphism [10], [11] only returns answers that exactly match with the given query graph Q (e.g., only u5 is returned for Q in Figure 1), while other semantically similar but structurally different answers are ignored (e.g., u6, u7, and u10). Analogously, a relational or SPARQL query finds answers matching exactly the schema of the input query, and other valid answers with different schemas will be ignored (see [12], [6], [13] and also our experimental results). In addition to exact matching, several other works [5], [14], [15], [16] return similar answers to Q. However, it is difficult for them to return 100% accurate answers (the notion of “accurate” answers could very well depend on the user’s query intension, or may even be vague [17], [18]). Calculating the aggregate result over answers with low quality leads to significant errors. Worse still, we lack an effective way to quantify the result’s quality. In addition, since an additional aggregate operation is applied on the factoid queries’ answers to obtain the aggregate result, factoid queries’ efficiency substantially affects aggregate queries’ efficiency.

Our solution: In practice, aggregate queries may not need a tardy exact result. It is more desirable if a query engine first quickly returns an approximate aggregate result with some accuracy guarantee (e.g., a confidence interval), while improving the accuracy as more time is spent [19], [20]. In this way, we can early terminate the query once the approximate result is acceptable. This improves the user’s experience and saves computing resources [6], [21], [22], [23]. In particular, we propose an iterative and approximate approach (Figure 1(c)) to efficiently answer aggregate queries over KGs, having an accuracy guarantee, but without requiring factoid query evaluations.

Due to the “schema-flexible” nature in KGs, we adopt the “semantic similarity” [6] to measure how semantically similar a candidate answer is to a query graph. Specifically, we leverage an offline KG embedding model [24], [25], [26] to represent predicates as d-dimensional vectors that can well capture their semantic meanings and measure the predicate similarity. On top of this, we design a semantic-aware sampling algorithm via a random walk on the KG. As a result, answers that are more semantically similar to Q would be sampled with higher probabilities than others with lower semantic similarities. We formally prove that the random walk converges, and all answers in a random sample are independent and identically distributed (i.i.d.) random variables. Next, we estimate an unbiased (or consistent) approximate aggregate result $\hat{V}$ based on the random sample, and provide an accuracy guarantee for $\hat{V}$ by iteratively computing a tight enough confidence interval CI $=[\hat{V} - ε , \hat{V} + ε]$ at a confidence level 1 - α, where ε is the half-width of a CI (also called the Margin of Error). A CI states that the ground truth $V$ is covered by an interval $\hat{V} ± ε$ with probability 1 - α. We terminate the query when a tight CI (with a small enough ε) is obtained, and ensure that the relative error of $\hat{V}$ is bounded by a user-specific error bound $e_b$. To the best of our knowledge, we are the first to use a “sampling-estimation” model to answer aggregate queries on KGs with an accuracy guarantee, together with iterative improvements in error bounds.

We also extend our solution to support complex aggregate queries with filter, GROUP-BY, and different graph shapes, e.g., chain, cycle, star, and flower [9]. We conducted thorough experiments over three diverse real-world KGs showing accuracy and efficiency improvements against state-of-the-art methods, and our approach’s effectiveness when a user varies the error bound interactively. A snippet of our experimental results are given in Tables 1 and 2.

TABLE 1: Effectiveness: relative error (%) for different query shapes over all datasets and all queries (human-annotated ground truth)

TABLE 2: Efficiency: average response time (ms) for different query shapes over all datasets and all queries

For more information, click here for our paper.  Code and datasets: [Link].

References

[1] J. Lehmann, R. Isele, M. Jakob, A. Jentzsch, D. Kontokostas, P. N. Mendes, S. Hellmann, M. Morsey, P. van Kleef, S. Auer, and C. Bizer, “DBpedia - A Large-Scale, Multilingual Knowledge Base Extracted from Wikipedia,” Semantic Web, vol. 6, no. 2, pp. 167–195, 2015.

[2] J. Hoffart, F. M. Suchanek, K. Berberich, and G. Weikum, “YAGO2: A Spatially and Temporally Enhanced Knowledge Base from Wikipedia,” Artificial Intelligence, vol. 194, pp. 28–61, 2013.

[3] K. D. Bollacker, C. Evans, P. Paritosh, T. Sturge, and J. Taylor, “Freebase: A Collaboratively Created Graph Database for Structuring Human Knowledge,” in SIGMOD, 2008.

[4] T. M. Mitchell, W. W. Cohen, E. R. H. Jr., P. P. Talukdar, B. Yang, J. Betteridge, A. Carlson, B. D. Mishra, M. Gardner, B. Kisiel, J. Krishnamurthy, N. Lao, K. Mazaitis, T. Mohamed, N. Nakashole, E. A. Platanios, A. Ritter, M. Samadi, B. Settles, R. C. Wang, D. Wijaya, A. Gupta, X. Chen, A. Saparov, M. Greaves, and J. Welling, “Never-Ending Learning,” Commun. ACM, vol. 61, no. 5, pp. 103–115, 2018.

[5] W. Zheng, L. Zou, W. Peng, X. Yan, S. Song, and D. Zhao, “Semantic SPARQL Similarity Search over RDF Knowledge Graphs,” PVLDB, vol. 9, no. 11, pp. 840–851, 2016.

[6] Y. Wang, A. Khan, T. Wu, J. Jin, and H. Yan, “Semantic Guided and Response Times Bounded Top-k Similarity Search over Knowledge Graphs,” in ICDE, 2020.

[7] E. Agichtein, S. Cucerzan, and E. Brill, “Analysis of Factoid Questions for Effective Relation Extraction,” in SIGIR, 2005.

[8] “QALD-4,” http://qald.aksw.org/index.php?x=challenge&q=4, 2014.

[9] A. Bonifati, W. Martens, and T. Timm, “An Analytical Study of Large SPARQL Query Logs,” PVLDB, vol. 11, no. 2, pp. 149–161, 2017.

[10] L. Zou, M. T. O¨ zsu, L. Chen, X. Shen, R. Huang, and D. Zhao, “gStore: A Graph-based SPARQL Query Engine,” VLDB J., vol. 23, no. 4, pp. 565–590, 2014.

[11] J. Cheng, J. X. Yu, B. Ding, S. Y. Philip, and H. Wang, “Fast Graph Pattern Matching,” in ICDE, 2008.

[12] S. Yang, Y. Wu, H. Sun, and X. Yan, “Schemaless and Structureless Graph Querying,” PVLDB, vol. 7, no. 7, pp. 565–576, 2014.

[13] A. Khan, N. Li, X. Yan, Z. Guan, S. Chakraborty, and S. Tao, “Neighborhood Based Fast Graph Search in Large Networks,” in SIGMOD, 2011.

[14] A. Khan, Y. Wu, C. C. Aggarwal, and X. Yan, “NeMa: Fast Graph Search with Label Similarity,” PVLDB, vol. 6, no. 3, pp. 181–192, 2013.

[15] S. Yang, F. Han, Y. Wu, and X. Yan, “Fast Top-k Search in Knowledge Graphs,” in ICDE, 2016.

[16] W. Fan, J. Li, S. Ma, H. Wang, and Y. Wu, “Graph Homomorphism Revisited for Graph Matching,” PVLDB, vol. 3, no. 1-2, pp. 1161–1172, 2010.

[17] M. Lissandrini, T. B. Pedersen, K. Hose, and D. Mottin, “Knowledge Graph Exploration: Where Are We and Where Are We Going?” ACM SIGWEB Newsletter, no. 4, 2020.

[18] Y. Wu and A. Khan, “Graph Pattern Matching,” in Encyclopedia of Big Data Technologies. Springer, 2019.

[19] N. Laptev, K. Zeng, and C. Zaniolo, “Early Accurate Results for Advanced Analytics on Mapreduce,” PVLDB, vol. 5, no. 10, pp. 1028–1039, 2012.

[20] S. Chaudhuri, B. Ding, and S. Kandula, “Approximate Query Processing: No Silver Bullet,” in SIGMOD, 2017.

[21] F. Li, B. Wu, K. Yi, and Z. Zhao, “Wander Join: Online Aggregation via Random Walks,” in SIGMOD, 2016.

[22] S. S. Bhowmick, B. Choi, and S. Zhou, “VOGUE: Towards A Visual Interaction-aware Graph Query Processing Framework,” in CIDR, 2013.

[23] S. Agarwal, B. Mozafari, A. Panda, H. Milner, S. Madden, and I. Stoica, “BlinkDB: Queries with Bounded Errors and Bounded Response Times on Very Large Data,” in Eurosys, 2013.

[24] A. Bordes, N. Usunier, A. Garc´ıa-Dur´an, J. Weston, and O. Yakhnenko, “Translating Embeddings for Modeling Multi-relational Data,” in NIPS, 2013.

[25] G. Ji, S. He, L. Xu, K. Liu, and J. Zhao, “Knowledge Graph Embedding via Dynamic Mapping Matrix,” in ACL, 2015.

[26] Z. Wang, J. Zhang, J. Feng, and Z. Chen, “Knowledge Graph Embedding by Translating on Hyperplanes,” in AAAI, 2014.