Measurements, Analyses, and Insights on the Entire Ethereum Blockchain Network

 Graph Classification with Minimum DFS Code: Improving Graph Neural Network Expressivity

A summary of the IEEE BigData 2021 research paper by Jhalak Gupta and Arijit Khan [presented in Machine Learning on Big Data (MLBD 2021), special session of IEEE BigData 2021].

Background: Graph Classification

Given a set of graphs with different structures and sizes, the graph classification problem predicts the class labels of unseen graphs [1, 2, 3]. Developing machine learning tools for classifying graphs can be found in cheminformatics [1, 4] and bioinformatics [6], malware detection [7], telecommunication networks, internet-of-things [8], trajectories and social networks [9]. This is challenging because network data contain graphs with different numbers of nodes and edges, and a generic node order is often not available. Graphs do not have regular grid structures, since the neighborhood size of each node differs. The lack of ordered vector representation complicates machine learning on graphs, and makes it difficult to build a classifier over the graph space [2, 3].

Graph Convolutional Neural Networks (GCNs)

Encouraged by the success of convolutional neural networks (CNNs) in computer vision, their end-to-end learning and ability to extract localized spatial features, a large number of graph convolutional neural networks (GCNs) [2, 3, 10, 11,  12] are recently developed. GCNs follow a recursive neighbors aggregation (or message passing) model. As one layer in the GCN aggregates its 1-hop neighbors, after k-rounds of aggregation, a node is represented by its feature vector that captures the structural information in its k-hop neighborhood. The graph feature is derived by a readout function or pooling on node features.

It is proven in [13, 14] that recent GNN variants are not powerful than the 1-WL (Weisfeiler Lehman) test [15, 16] in distinguishing non-isomorphic graphs, where the WL test is a necessary but insufficient condition for graph isomorphism [17], thus limiting their abilities to adequately exploit graph structures. Our work is motivated by the following question: Can we improve the discriminative/representational power of GNNs than the existing GCNs?

Our Solution: Minimum DFS Code and RNN/ Transformer-based Graph Classification

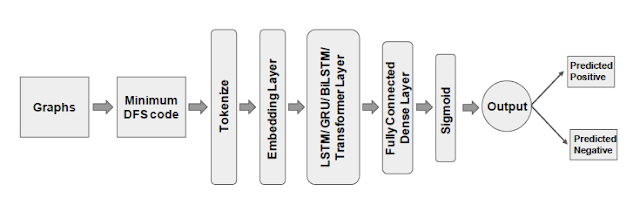
We employ the minimum DFS code [19] that is a canonical form of a graph, and captures the graph structure precisely along with node and edge labels. The canonical form of a graph is a sequence – two graphs are isomorphic iff they have the same canonical form. Minimum DFS code encodes a graph into a unique edge sequence by doing a depth-first search (DFS). Constructing the minimum DFS code is equivalent to solving graph isomorphism, and it has the worst-case computation cost of O(n!), n being the number of nodes. However, real-world graphs are sparse and have node and edge labels, which prune the search space significantly, thus we can efficiently compute the minimum DFS code in practice [18, 19, 20, 21].

Due to the sequential nature of the minimum DFS code, we employ state-of-the-art RNN-based sequence classification techniques (Long short-term memory (LSTM) [22], Bidirectional LSTM (BiLSTM) [23], and Gated recurrent unit (GRU) [24]) and Transformers [25] for downstream graph classification. Our RNN and Transformer-based sequence classification over minimum DFS codes has following benefits compared to existing GCNs, which employ adjacency matrix-based graph representations (e.g., graph Laplacian and degree matrices). (i) LSTM, BiLSTM, GRU, and Transformers can captures long-term dependencies in arbitrary-length sequences, and have achieved great success in a wide range of sequence learning tasks including language modeling and speech recognition [28]. On the other hand, a deep GCN with many convolutional layers suffers from the over-smoothing problem, and generally cannot capture long-range interactions [26, 27]. (ii) The minimum DFS code is unique for all isomorphic graphs, whereas there are O(n!) mappings from a graph to its adjacency matrix, therefore GCN designs must be node permutation-invariant.

Figure-1: Minimum DFS code-based graph classification

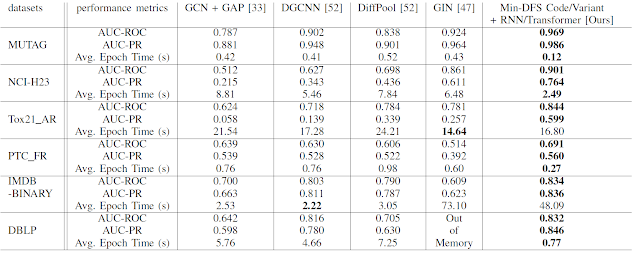
Our framework is presented in Figure 1. We additionally consider a novel variant of the minimum DFS code, which further improves the classification accuracy. Table 1 reports our accuracy and efficiency comparison results with four existing GCNs [12]: GCN+GAP [5, 11], DGCNN [2], DiffPool [3], and GIN [13].

Table-1: Comparison of Minimum DFS Code-based Graph Classification with existing GCNs

For more information, click here for our paper.  Datasets: GitHub.

References

[1] D. Duvenaud, D. Maclaurin, J. A.-Iparraguirre, R. G.-Bombarelli, T. Hirzel, A. A.-Guzik, and R. P. Adams, “Convolutional Networks on Graphs for Learning Molecular Fingerprints,” NeurIPS, 2015.

[2] M. Zhang, Z. Cui,M. Neumann, and Y. Chen, “An End-to-End Deep Learning Architecture for Graph Classification,” AAAI, 2018.

[3] Z. Ying, J. You, C. Morris, X. Ren, W. L. Hamilton, and J. Leskovec, “Hierarchical Graph Representation Learning with Differentiable Pooling,” NeurIPS, 2018.

[4] Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing, and V. S. Pande, “MoleculeNet: A Benchmark for Molecular Machine Learning,” CoRR abs/1703.00564, 2017.

[5] P. E. Pope, S. Kolouri, M. Rostami, C. E. Martin, and H. Hoffmann, “Explainability Methods for Graph Convolutional Neural Networks,” CVPR, 2019.

[6] R. Sharan, S. Suthram, R. M. Kelley, T. Kuhn, S. McCuine, P. Uetz, T. Sittler, R. M. Karp, and T. Ideker, “Conserved Patterns of Protein Interaction in Multiple Species,” PNAS, vol. 102, no. 6, 2005.

[7] M. Fan, X. Luo, J. Liu, M. Wang, C. Nong, Q. Zheng, and T. Liu, “Graph Embedding based Familial Analysis of Android Malware using Unsupervised Learning,” ICSE, 2019.

[8] K. Ding, J. Li, R. Bhanushali, and H. Liu, “Deep Anomaly Detection on Attributed Networks,” SDM, 2019.

[9] W. L. Hamilton, R. Ying, and J. Leskovec, “Representation Learning on Graphs: Methods and Applications,” IEEE Data Eng. Bull., vol. 40, no. 3, 2017.

[10] T. N. Kipf and M. Welling, “Semi-Supervised Classification with Graph Convolutional Networks,” ICLR, 2017.

[11] M. Lin, Q. Chen, and S. Yan, “Network In Network”, ICLR, 2014.

[12] F. Errica, M. Podda, D. Bacciu, and A. Micheli, “A Fair Comparison of Graph Neural Networks for Graph Classification,” ICLR, 2020.

[13] K. Xu, W. Hu, J. Leskovec, and S. Jegelka, “How Powerful are Graph Neural Networks?” ICLR, 2019.

[14] C. Morris, M. Ritzert, M. Fey, W. L. Hamilton, J. E. Lenssen, G. Rattan, and M. Grohe, “Weisfeiler and Leman Go Neural: Higher-Order Graph Neural Networks,” AAAI, 2019.

[15] B. Weisfeiler and A. A. Lehman, “A Reduction of a Graph to a Canonical Form and an Algebra Arising During This Reduction,” Nauchno-Technicheskaya Informatsia, vol. 2, no. 9, 12–16, 1968.

[16] H. L. Morgan, “The Generation of a UniqueMachine Description for Chemical Structures - A Technique Developed at Chemical Abstracts,” Service. J. Chem. Document, vol. 5, no. 2, 107–113, 1965.

[17] J. Cai, M. F¨urer, and N. Immerman, “An Optimal Lower Bound on the Number of Variables for Graph Identifications,” Comb., vol. 12, no. 4, 389–410, 1992.

[18] A. Prateek, A. Khan, A. Goyal, and S. Ranu, “Mining Top-k Pairs of Correlated Subgraphs in a Large Network,” PVLDB, vol. 13, no. 9, 1511–1524, 2020.

[19] X. Yan and J. Han, “gSpan: Graph-Based Substructure Pattern Mining,” ICDM, 2002.

[20] N. Goyal, H. V. Jain, and S. Ranu, “GraphGen: A Scalable Approach to Domain-agnostic Labeled Graph Generation,” WWW, 2020.

[21] X. Liu, H. Pan, M. He, Y. Song, X. Jiang, and L. Shang, “Neural Subgraph Isomorphism Counting,” KDD, 2020.

[22] S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural computation, vol. 9, no. 8, 1735–1780, 1997.

[23] M. Schuster and K. K. Paliwal, “Bidirectional Recurrent Neural Networks,” IEEE Trans. Signal Process., vol. 45, no. 11, 2673–2681, 1997.

[24] K. Cho, B. van Merrienboer, C¸ . G¨ulc¸ehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation,” EMNLP, 2014.

[25] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin, “Attention is All you Need,” NeurIPS, 2017.

[26] U. Alon and E. Yahav, “On the Bottleneck of Graph Neural Networks and its Practical Implications,” CoRR abs/2006.05205, 2020.

[27] Q. Li, Z. Han, and X.-M. Wu, “Deeper Insights Into Graph Convolutional Networks for Semi-Supervised Learning,” AAAI, 2018.

[28] Z. Wang, Y. Ma, Z. Liu, and J. Tang, “R-Transformer: Recurrent Neural Network Enhanced Transformer,” CoRR abs/1907.05572, 2019.