Shortest Paths and Centrality in Uncertain Networks
A summary of the PVLDB 2021 research paper by Arkaprava Saha, Ruben Brokkelkamp, Yllka Velaj, Arijit Khan, and Francesco Bonchi
[Background: Uncertain Graph and Shortest Path] Uncertain networks, i.e., graphs where each edge is associated with a probability of existence, have received a great deal of attention thanks to their expressivity and applicability in many real world contexts. Uncertainty in a network might arise due to noisy measurements [2], edge imputation using inference and prediction models [1, 3], and explicit manipulation of edges, e.g., for privacy purposes [4]. Researchers have studied 𝑘-nearest neighbor queries [5, 6], reachability queries [7], clustering [8], sampling [9], network design [10], and embedding [11], just to mention a few.
Shortest-path queries [12, 13, 14], on the other hand, are one of the fundamental graph primitives with a plethora of applications, e.g., traffic routing, finding functional pathways in biological networks. A critical application of shortest paths is the computation of betweenness centrality [15, 16, 17, 18], a measure of importance of a node based on its effectiveness in connecting pairs of other nodes via shortest paths.
[Our Problem: Most Probable Shortest Path (MPSP) and Betweenness Centrality in Uncertain Graph] We first study the fundamental problem of computing shortest-path queries in uncertain networks, then we build over it a measure of betweeness centrality. The notion of shortest path in an uncertain graph should consider not only the length of a path but also the probability of existence of all edges on the path. Specifically, given an uncertain graph G, a source node 𝑠, and a target node 𝑡, our goal is to find the path 𝑃 from 𝑠 to 𝑡 with the highest probability of being the shortest path (SP), i.e., the probability with which 𝑃 exists and no path shorter than 𝑃 exists. We refer to such a path as the Most Probable Shortest Path (MPSP) from 𝑠 to 𝑡.
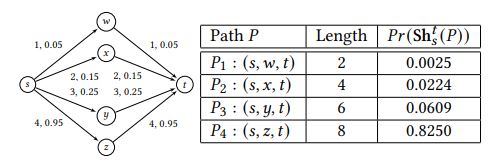
Figure 1: Example of paths in an uncertain graph: 𝑃𝑟 (Sh^𝑡_𝑠 (𝑃)) denotes the probability that path 𝑃 is the shortest path from 𝑠 to 𝑡.Each edge in the uncertain graph in Figure 1 is annotated with its length and its probability of existence. For the source 𝑠 and target 𝑡, although the path 𝑃1 = (𝑠,𝑤, 𝑡) is the shortest (when not considering probabilities), the one having the highest probability of being the shortest path, i.e., the MPSP from 𝑠 to 𝑡, is 𝑃4 = (𝑠, 𝑧, 𝑡), which is also the longest path (when not considering probabilities).
[Applications] Computing MPSPs is useful in many applications. Road networks are modeled as uncertain graphs because of unexpected traffic jams [19], where a vehicle driver may find the MPSP to the nearest gas station or restaurant. MPSPs are also useful in routing over wireless sensor networks, where links between sensor nodes have a probability of failure. Many applications not only require the shortest route, but also one with a high precision [20, 21], such as being the shortest with a high probability. Brain networks are often represented as weighted uncertain graphs, where nodes are the brain regions of interest (ROIs), edges indicate potential coactivation between ROIs, edge distance represents physical distance between ROIs, and edge probability indicates the strength of the co-activation signal [22]. Finding MPSPs between different ROIs of the brain could differentiate healthy brains from those with diseases, such as autism [23, 24]. In our paper, we present two concrete use cases of MPSPs on sensor networks and brain networks.
[Technical Contributions] We formally define the concept of the Most Probable Shortest Path (MPSP) in an uncertain graph, prove that our problem is #P-hard, and also derive other interesting properties highlighting the complexity of computing MPSPs. Many of the classical properties of shortest paths over deterministic graphs no longer hold for MPSPs in uncertain graphs. For instance, the concatenation of two MPSPs, and a subpath of an MPSP, are not necessarily MPSPs.
We then discuss an earlier baseline solution [25], together with its shortcomings. Next, we propose our sampling based efficient algorithms, with end-to-end accuracy guarantees, to compute the MPSP. In particular, we propose a two-phase algorithm to approximate the MPSP between two nodes in an uncertain graph. In the first phase we compute paths that are candidates for being the MPSP (via Dijkstra+Monte-Carlo sampling), and in the second phase we approximate the probability of each candidate path being the shortest path (via Luby-Karp algorithm [26]). Dijkstra+MC is simple, yet effective and efficient for candidate generation: In Figure 1, there are four paths from 𝑠 to 𝑡. The path 𝑃4 (the longest path) is the MPSP. The probabilities of the edges in 𝑃4 are much larger than those of the edges in the other paths. Hence, a run of Dijkstra+MC on this graph produces the path 𝑃4 with a higher probability, since the other edges are highly unlikely to be sampled. Thus, we need only a small number of such runs (maybe 1 or 2) to include 𝑃4 in the candidate set. On the other hand, the method in [25] requires all the three remaining paths to be enumerated before 𝑃4, which is clearly more time-consuming.
We then focus on three important generalizations of our problem: first we study top-𝑘 MPSP queries for 𝑘 > 1; followed by single-source and single-target MPSP queries; then MPSPs over uncertain multi-graphs. The last one provides a general data model, since it allows one to model the uncertainty as a probability distribution of the length of an edge: for instance, in road networks, it can model the probability distribution of travel times on specific road segments. Furthermore, we study MPSP-Betweenness-Centrality and develop efficient sampling strategies to compute the top-𝑘 central nodes, with theoretical quality guarantees.
[Case Study: Brain Network] A brain network can be defined as a weighted uncertain graph, where nodes are brain regions of interest (ROIs), (bi-directed) edges indicate co-activation between ROIs, edge distance represents physical distance between ROIs, and edge probability indicates the strength of the co-activation signal (i.e., the pairwise Pearson correlation between the time series of each pair of ROIs). We use a publicly available dataset from the Autism Brain Imaging Data Exchange (ABIDE) project [22]. The dataset contains data of 52 Typically Developed (TD) children and 49 children suffering from Autism Spectrum Disorder (ASD) whose age is at most 9 years [27, 28, 29, 30]: each subject corresponds to a graph over 116 nodes (ROIs).
Figure 2: MPSPs for TD group (left) and ASD group (right) of brain networks. Each of 4 MPSPs is represented by edges of same color.
Figure 3: MPSPs for TD group (left) and ASD group (right) of brain networks. Each of 2 MPSPs is represented by edges of same color.
G_{𝐴𝑆𝐷} and G_{𝑇𝐷} are weighted uncertain graphs, defined over the same set of nodes as the original graphs, while the weight and probability of each edge are the averages of the respective values of the same edge across all graphs in the ASD and TD groups. In Figures 2 and 3, we show the MPSPs for 6 𝑠-𝑡 pairs of both G_{𝑇𝐷} (left) and G_{𝐴𝑆𝐷} (right). Consider the pink path in Figure 2 from the inferior frontal gyrus, opercular part (IFGoperc.L) to the cerebellum (CRBL1). The MPSP in G_{𝑇𝐷} is a path with 2 hops over a longer distance, compared to that in G_{𝐴𝑆𝐷} with 6 shorter hops. This is consistent with the results of different works in neuroscience [23, 31] indicating that ASD is characterized by underconnectivity between distant brain regions and overconnectivity between closer ones. Moreover, children with ASD have brains that are overly connected compared to typically developed children [24, 32, 33]. In addition, the hemispheres in ASD group are more symmetrical than those of the TD group [34]. We highlight this in Figure 3: the MPSPs in the left and right cerebral hemispheres of the brain are indeed more similar and symmetrical in children with autism, while in the TD group the paths can cross the hemispheres and also span the same regions. Our consistent findings underline the importance of MPSPs in uncertain graphs.
For more information, click here for our paper. Code: GitHub.
References
[1] Eytan Adar and Christopher Re. 2007. Managing uncertainty in social networks. IEEE Data Engineering Bulletin 30, 2 (2007), 15–22.
[2] Charu C. Aggarwal. 2009. Managing and Mining Uncertain Data. Advances in Database Systems, Vol. 35. Springer, Boston, MA, USA.
[3] David Liben-Nowell and Jon Kleinberg. 2003. The link prediction problem for social networks. In Proceedings of the Twelfth ACM International Conference on Information and Knowledge Management (New Orleans, LA, USA) (CIKM ’03). Association for Computing Machinery, New York, NY, USA, 556–559. https: //doi.org/10.1145/956863.956972.
[4] Paolo Boldi, Francesco Bonchi, Aristides Gionis, and Tamir Tassa. 2012. Injecting uncertainty in graphs for identity obfuscation. Proceedings of the VLDB Endowment (PVLDB) 5, 11 (July 2012), 1376–1387. https://doi.org/10.14778/2350229. 2350254.
[5] Xiaodong Li, Reynold Cheng, Yixiang Fang, Jiafeng Hu, and Silviu Maniu. 2018. Scalable evaluation of k-NN queries on large uncertain graphs. In Proceedings of the 21st International Conference on Extending Database Technology (EDBT 2018). Vienna, Austria, 181–192. https://doi.org/10.5441/002/edbt.2018.17.
[6] Michalis Potamias, Francesco Bonchi, Aristides Gionis, and George Kollios. 2010. K-nearest neighbors in uncertain graphs. Proceedings of the VLDB Endowment (PVLDB) 3, 1-2 (2010), 997–1008.
[7] Xiangyu Ke, Arijit Khan, and Leroy Lim Hong Quan. 2019. An in-depth comparison of s-t reliability algorithms over uncertain graphs. Proceedings of the VLDB Endowment (PVLDB) 12, 8 (April 2019), 864–876. https://doi.org/10.14778/ 3324301.3324304.
[8] Kai Han, Fei Gui, Xiaokui Xiao, Jing Tang, Yuntian He, Zongmai Cao, and He Huang. 2019. Efficient and effective algorithms for clustering uncertain graphs. Proceedings of the VLDB Endowment (PVLDB) 12, 6 (2019), 667–680.
[9] Panos Parchas, Francesco Gullo, Dimitris Papadias, and Franceseco Bonchi. 2014. The pursuit of a good possible world: Extracting representative instances of uncertain graphs. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. Association for Computing Machinery, New York, NY, USA, 967–978.
[10] Xiangyu Ke, Arijit Khan, Mohammad Al Hasan, and Rojin Rezvansangsari. 2020. Reliability maximization in uncertain graphs. IEEE Transactions on Knowledge and Data Engineering (2020).
[11] Jiafeng Hu, Reynold Cheng, Zhipeng Huang, Yixang Fang, and Siqiang Luo. 2017. On embedding uncertain graphs. In Proceedings of the 2017 ACM International Conference on Information and Knowledge Management (CIKM 2017). Association for Computing Machinery, New York, NY, USA, 157–166.
[12] Francesco Bonchi, Aristides Gionis, Francesco Gullo, and Antti Ukkonen. 2014. Distance oracles in edge-labeled graphs. In Proceedings of the 17th International Conference on Extending Database Technology (EDBT 2014). 547–558.
[13] David Eppstein. 1998. Finding the k shortest paths. SIAM J. Comput. 28, 2 (1998), 652–673.
[14] Donald B. Johnson. 1977. Efficient algorithms for shortest paths in sparse networks. Journal of the ACM (JACM) 24, 1 (1977), 1–13.
[15] Ulrik Brandes. 2001. A faster algorithm for betweenness centrality. Journal of Mathematical Sociology 25, 2 (2001), 163–177.
[16] Linton C. Freeman. 1977. A set of measures of centrality based on betweenness. Sociometry 40, 1 (1977), 35–41.
[17] Ahmad Mahmoody, Charalampos E Tsourakakis, and Eli Upfal. 2016. Scalable betweenness centrality maximization via sampling. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery, New York, NY, USA, 1765–1773.
[18] Matteo Riondato and Evgenios M. Kornaropoulos. 2016. Fast approximation of betweenness centrality through sampling. Data Mining and Knowledge Discovery 30, 2 (2016), 438–475.
[19] Ming Hua and Jian Pei. 2010. Probabilistic path queries in road networks: Traffic uncertainty aware path selection. In Proceedings of the 13th International Conference on Extending Database Technology. 347–358.
[20] Joy Ghosh, Hung Q. Ngo, Seokhoon Yoon, and Chunming Qiao. 2007. On a routing problem within probabilistic graphs and its application to intermittently connected networks. In IEEE INFOCOM 2007-26th IEEE International Conference on Computer Communications. IEEE, 1721–1729.
[21] Arijit Khan, Francesco Bonchi, Aristides Gionis, and Francesco Gullo. 2014. Fast reliability search in uncertain graphs.. In Proceedings of the 17th International Conference on Extending Database Technology (EDBT 2014). 535–546.
[22] Cameron Craddock, Yassine Benhajali, Carlton Chu, Francois Chouinard, Alan Evans, András Jakab, Budhachandra Singh Khundrakpam, John David Lewis, Qingyang Li, Michael Milham, Chaogan Yan, and Pierre Bellec. 2013. The neuro bureau preprocessing initiative: Open sharing of preprocessed neuroimaging data and derivatives. Frontiers in Neuroinformatics (2013). https://doi.org/10. 3389/conf.fninf.2013.09.00041.
[23] Adriana Di Martino, Clare Kelly, Rebecca Grzadzinski, Xi-Nian Zuo, Maarten Mennes, María Mairena, Catherine Lord, Francisco Castellanos, and Michael Milham. 2010. Aberrant striatal functional connectivity in children with autism. Biological Psychiatry 69, 9 (12 2010), 847–56. https://doi.org/10.1016/j.biopsych. 2010.10.029.
[24] Luis García Domínguez, Jim Stieben, José Luis Pérez Velázquez, and Stuart Shanker. 2013. The imaginary part of coherency in autism: Differences in cortical functional connectivity in preschool children. PLOS ONE 8, 10 (10 2013), 1–13. https://doi.org/10.1371/journal.pone.0075941.
[25] Lei Zou, Peng Peng, and Dongyan Zhao. 2011. Top-K possible shortest path query over a large uncertain graph. In International Conference on Web Information Systems Engineering (WISE 2011). Springer, Berlin, Heidelberg, 72–86.
[26] Richard M. Karp and Michael Luby. 1983. Monte-Carlo algorithms for enumeration and reliability problems. In 24th Annual Symposium on Foundations of Computer Science (SFCS 1983). IEEE, 56–64.
[27] Sadamori Kojaku and Naoki Masuda. 2019. Constructing networks by filtering correlation matrices: A null model approach. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 475, 2231 (2019), 20190578. https://doi.org/10.1098/rspa.2019.0578.
[28] Tommaso Lanciano, Francesco Bonchi, and Aristides Gionis. 2020. Explainable classification of brain networks via contrast subgraphs. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 11. https://doi.org/10.1145/3394486.3403383.
[29] Naoki Masuda, Sadamori Kojaku, and Yukie Sano. 2018. Configuration model for correlation matrices preserving the node strength. Physical Review E 98 (Jul 2018), 012312. Issue 1. https://doi.org/10.1103/PhysRevE.98.012312.
[30] Nathalie Tzourio-Mazoyer, Brigitte Landeau, Dimitri Papathanassiou, Fabrice Crivello, Olivier Etard, Nicolas Delcroix, Bernard Mazoyer, and Marc Joliot. 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage 15, 1 (2002), 273 – 289. https://doi.org/10.1006/nimg.2001.0978.
[31] Sarah Noonan, Frank Haist, and Ralph-Axel Müller. 2009. Aberrant functional connectivity in autism: Evidence from low-frequency BOLD signal fluctuations. Brain Research 1262 (02 2009), 48–63. https://doi.org/10.1016/j.brainres.2008.12. 076.
[32] Christopher Keown, Patricia Shih, Aarti Nair, Nick Peterson, Mark Mulvey, and Ralph-Axel Müller. 2013. Local functional overconnectivity in posterior brain regions is associated with symptom severity in autism spectrum disorders. Cell Reports 5 (11 2013), 567–572. https://doi.org/10.1016/j.celrep.2013.10.003.
[33] Kaustubh Supekar, Lucina Q. Uddin, Amirah Khouzam, Jennifer Phillips, William D. Gaillard, Lauren E. Kenworthy, Benjamin E. Yerys, Chandan J. Vaidya, and Vinod Menon. 2013. Brain hyperconnectivity in children with autism and its links to social deficits. Cell Reports 5, 3 (2013), 738 – 747. https://doi.org/10.1016/j.celrep.2013.10.001.
[34] Merel Postema, Daan Van Rooij, Evdokia Anagnostou, Celso Arango, Guillaume Auzias, Marlene Behrmann, Geraldo Busatto, Sara Calderoni, Rosa Calvo, Eileen Daly, Christine Deruelle, Adriana Di Martino, Ilan Dinstein, Fabio Duran, Sarah Durston, Christine Ecker, Stefan Ehrlich, Damien Fair, Jennifer Fedor, and Clyde Francks. 2019. Altered structural brain asymmetry in autism spectrum disorder in a study of 54 datasets. Nature Communications 10 (12 2019). https://doi.org/ 10.1038/s41467-019-13005-8.




Comments
Post a Comment